А как насчет πe, π/e и π-e? Оно также неизвестно, и знание этого факта, безусловно, очень важно для теории чисел. Трансцендентность чисел была доказана в конце XIX века Фердинандом фон Линдеманом, как и невозможность решения задачи о квадратуре круга. С тех пор существенного прогресса в решении этого вопроса не достигнуто.
Недоказанные теоремы современности, за которые полагается награда
Иногда прилежное изучение точных наук может принести свои плоды — вы не только становитесь всемирно известным, но и богатым. Однако премии не даются даром, и в современной науке существует множество недоказанных теорий, теорем и проблем, которые множатся с развитием науки, достаточно вспомнить тетради Коуровского или Днестровских, такие сборники нерешенных физико-математических, и не только, проблем. Однако есть действительно сложные теоремы, которые не могут быть решены в течение десятилетий, и именно поэтому Американский институт глины присудил премию в размере 1 миллиона долларов за каждую из этих теорем. В 2002 году джекпот составлял 7 миллионов, потому что было семь задач тысячелетия, но российский математик Григорий Перельман решил задачу «Предположение Пуанкаре», эпично отдав миллион, даже не открыв дверь американским математикам, которые хотели отдать ему честно выигранные деньги. Так что давайте возьмем «Теорию большого взрыва» в качестве фона и настроения и посмотрим, из чего еще можно выкроить круглую сумму.
Равенство классов P и NP
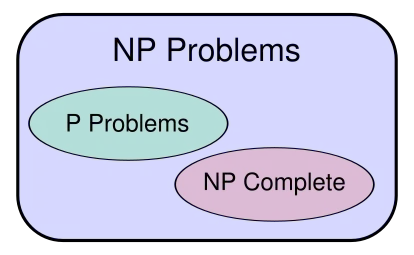
Проще говоря, проблема равенства P = NP заключается в следующем: если положительный ответ на вопрос можно проверить достаточно быстро (за полиномиальное время), то верно ли, что ответ на этот вопрос можно найти достаточно быстро (также за полиномиальное время и с полиномиальной памятью)? Другими словами: Не проще ли проверить решение проблемы, чем найти его? Дело в том, что определенные вычисления и расчеты легче решить с помощью алгоритма, чем перебором, что позволяет сэкономить много времени и ресурсов.
Гипотеза Ходжа
Догадка Ходжа была сформулирована в 1941 году и заключается в том, что для особенно хороших типов пространств, называемых проективными алгебраическими многообразиями, так называемые круги Ходжа являются комбинациями геометрически интерпретируемых объектов — алгебраических кругов.
Упрощенно можно сказать следующее: в 20 веке были открыты очень сложные геометрические формы, например, изогнутые бутылки. Поэтому было предложено, что для построения этих объектов для описания нужно применять довольно головоломные формы, не имеющие геометрического содержания, «такие ужасные многомерные шарики», или мы можем сделать это с помощью обычной формальной алгебры+геометрии.

Некоторые математические задачи нерешаемы, и это не так уж плохо

Постройте выпуклый восьмиугольник с четырьмя прямыми углами.
Наверное, это многое говорит обо мне как об учителе, что я ставлю такие задачи. Я наблюдаю, как студенты пытаются расставить прямые углы по порядку. Если у них не получается, они пытаются соединить прямые углы. В случае неудачи они вставляются в многоугольник случайным образом. Шум, который издает их мозг, когда они пытаются думать, — это музыка для ушей учителя.
Тогда они становятся подозрительными и начинают задавать вопросы. «Вы что-то говорили о прямых углах. Вы действительно имели в виду три угла?», «Вы уверены, что имели в виду выпуклый многоугольник?», «Четыре прямых угла на самом деле образуют прямоугольник. Как мы можем получить еще четыре стороны восьмиугольника?». Я внимательно слушаю и киваю, подтверждая ее предположения. Наконец-то кто-то задает вопрос, который никто не осмеливался задать, вопрос, которого я ждал: «Слушай, а это возможно?»
Этот вопрос способен изменить наше представление о математике. Те, кто раньше думал узко об определенных условиях, теперь должны думать более широко о том, как эти условия связаны между собой. Те, кто работает в системе, должны сделать шаг назад и посмотреть на саму систему. На протяжении всей истории математики этот вопрос задавался снова и снова, он озадачивал тех, кто решал задачу о квадратуре круга, чтобы обогнуть город Кенигсберг. И этот вопрос позволяет нам сформулировать, что такое математика и как мы ее понимаем.
Найти восьмиугольник с определенными свойствами — это совсем другое, чем доказать, что такого восьмиугольника не может существовать. Если мы поэкспериментируем с разными восьмиугольниками, мы можем найти восьмиугольник с четырьмя прямыми углами.
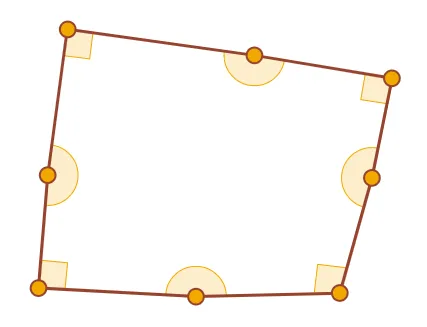
Это не пример. На самом деле этот восьмиугольник не имеет четырех прямых углов.
Но случайность не играет никакой роли в доказательстве того, что такой восьмиугольник не может существовать. Это требует глубоких знаний не только многоугольников, но и самой математики. Чтобы объяснить невозможность, нам нужно понять, что простое предположение о существовании объекта не доказывает его существования. Математические определения, свойства и теоремы находятся под давлением, потому что они взаимосвязаны. Пытаясь изобразить восьмиугольник с четырьмя прямыми углами, мы запутываемся в этих взаимосвязанных правилах.
Но чтобы понять, что восьмиугольник невозможен, мы должны сделать шаг назад и посмотреть на общую картину. Какие математические и геометрические принципы может нарушать восьмиугольник с четырьмя прямыми углами? Хорошей отправной точкой является теорема о сумме углов многоугольника.
Сумма внутренних углов многоугольника с n сторонами определяется по формуле:
Любой многоугольник с n сторонами можно разложить на ( n — 2) треугольников, где сумма внутренних углов каждого треугольника равна 180º.
В случае восьмиугольника это означает, что сумма внутренних углов равна (8 — 2) × 180º = 6 × 180º = 1080º. Если четыре угла прямые, т.е. каждый угол равен 90º, то общая сумма углов равна 4 × 90º = 360º. Это оставляет 1080º — 360º = 720º для остальных четырех углов восьмиугольника.
Такого треугольника не существует. Длины сторон не соответствуют теореме о неравенстве треугольника, которая гласит, что сумма любых двух сторон должна быть больше третьей. Это можно доказать геометрически: Возьмите отрезок длиной 85 и постройте на его концах окружности радиусами 38 и 46. Эти окружности не пересекаются, поэтому найти третью вершину треугольника невозможно.
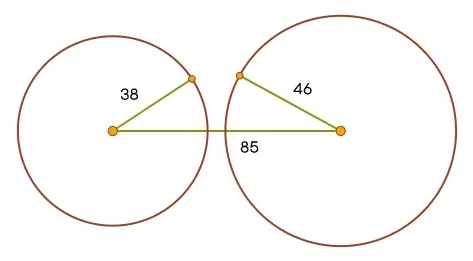
Будет интересно применить формулу Герона для вычисления площади этого не треугольника. Из этого возникнут интересные вопросы!
Существует несколько способов определить невозможность такого полинома. Например, эти условия нарушают теорему о рациональных корнях, которая гласит, что любой рациональный корень многочлена должен быть отношением делителя свободного члена (d) к делителю первого множителя (2).
Любопытный факт о полных квадратах доказывает, что эта проблема невозможна. При делении полного квадрата могут встречаться только цифры 0, 1, 4, 5, 6 или 9. Это можно доказать, возведя в квадрат все возможные цифры и наблюдая за возможными результатами. Поскольку ни один полный квадрат не может заканчиваться цифрами 2, 3, 7 или 8, не существует полного квадрата, состоящего только из этих цифр.
На правах рекламы
Какой бы ни была ваша проблема, всегда полезно иметь доступные и надежные серверы. Даже для сложных математических расчетов максимальная конфигурация — 128 ядер CPU, 512 ГБ RAM, 4000 ГБ NVMe.
Проблема Гольдбаха (бинарная)
Другая проблема заключается в том, что любое четное число (больше 2) можно представить в виде суммы двух простых чисел. И это краеугольный камень современной математики. Это утверждение легко проверить в голове для небольших значений: 18=13+5, 42=23+19. Если посмотреть на последнее, то можно довольно быстро понять глубину проблемы, потому что 42 появляется как 37+5 и 11+31, а также как 13+29 и 19+23. Для чисел больше тысячи количество пар членов становится огромным. Это очень важно для криптографии, но даже самые мощные суперкомпьютеры не могут исследовать все значения до бесконечности, поэтому необходимо явное доказательство для всех натуральных чисел.
Эта проблема была сформулирована Христианом Гольдбахом в его переписке с Леонардом Ойлером, другим великим представителем математики, в 1742 году. Сам Кристиан сформулировал вопрос несколько проще: «Любое нечетное число больше 5 можно представить в виде суммы трех простых чисел». В 2013 году перуанский математик Харальд Хельфготт нашел окончательное решение этой проблемы. Однако следствие из этого утверждения, предложенного Эйлером, которое называется «бинарной проблемой Гольдбаха», до сих пор никем не раскрыто.
Гипотеза о числах-близнецах
Числа-близнецы называются простыми числами, которые отличаются только на 2. Например, 11 и 13, или 5 и 3, или 599 и 601. Если бесконечность простых чисел была доказана многократно с древности, то бесконечность чисел-близнецов находится под вопросом. Начиная с 2, между первичными числами нет четных чисел, а начиная с 3, нет чисел, кратных трем. Следовательно, количество возможных близнецов становится все меньше и меньше, если убрать из серии все те, которые соответствуют «правилам деления». Единственным модулем для формулы нахождения таких чисел является 6, и формула выглядит следующим образом: 6n±1.
Как всегда в математике, когда проблему нельзя решить в лоб, ее решают с другой стороны. В 2013 году, например, было показано, что количество простых чисел, отличающихся на 70 миллионов, бесконечно. Менее чем через месяц значение разности увеличилось до 59 470 640, а затем на порядок — до 4 982 086. Существуют теоретические обоснования бесконечных пар простых чисел с разностью 12 и 6, но доказана только разность 246. Как и другие проблемы такого рода, гипотеза близнецовых чисел имеет особое значение для криптографии.
Гипотеза Римана
Вкратце, Бернхард Риман предложил, что распределение простых чисел в множестве всех натуральных чисел не подчиняется никакому закону. Однако их количество на определенном участке числовой прямой коррелирует с распределением определенных значений на графике дзета-функции. Например, если s заменить на 2, то получится уже решенная «базельская задача» — набор обратных квадратов (1 + 1/4 + 1/9 + 1/16 + … ).
Одна из «проблем тысячелетия», за решение которой предлагается приз в миллион долларов, а также включение в пантеон «богов» современной математики. На самом деле, доказательство этой гипотезы продвинет теорию чисел настолько, что это событие по праву можно будет назвать историческим. Многие вычисления и утверждения в математике основаны на предположении, что «гипотеза Римана» верна, и до сих пор она никого не разочаровала. Немецкий математик сформулировал знаменитую проблему 160 лет назад, и с тех пор ее решали бесчисленное количество раз, но прогресс был очень скромным.








