На основной шкале линейного тела (второй снизу) выберите первый фактор и установите начало нижней основной шкалы ползунка на этот фактор (который находится на передней части ползунка и точно соответствует основной шкале тела).
Предок калькулятора, без батареек: как правильно пользоваться логарифмической линейкой
Логарифмическая шкала — это универсальный калькулятор, который можно использовать для умножения, деления, приведения к квадрату и кубу, вычисления квадратных корней, кубических корней, синусов, тангенсов и многого другого. До появления калькуляторов, компьютеров и смартфонов инженеры носили журнальные линейки на поясе, а линейка «Pickett» даже летала с астронавтами на Луну.
Уильям Отред — изобретатель логарифмической линейки
Уильям Отред, выпускник Итонской школы и Королевского колледжа в Кембридже, служитель церкви в Оллсбери, Суррей, был страстным математиком и с удовольствием передавал свой любимый предмет своим многочисленным ученикам, от которых не требовал никакого вознаграждения. «Небольшого роста, черноволосый и черноглазый, с острым взглядом, он постоянно что-то обдумывал, чертил линии и диаграммы в пыли, — описывал Отреда один из его биографов, — Всякий раз, когда он сталкивался с математической проблемой, представлявшей особый интерес, он не ел и не спал, пока не решал ее. Он является изобретателем логарифмической линейки.

История изобретения
В 1631 году Отред опубликовал самую важную работу своей жизни, руководство Clavis Mathematicae («Ключ к математике»), которое переиздавалось несколько раз на протяжении почти двух столетий. Однажды, обсуждая со своим учеником Уильямом Форстером «механические расчеты» с помощью линейки Гунтера, Отред указал на неадекватность метода. Тем временем учитель показал свое изобретение — несколько концентрических колец с логарифмическими шкалами и двумя стрелками на них.
Форстер был очарован и позже написал: «Это было лучше, чем любой другой инструмент, который я знал. Я задавался вопросом, почему он скрывал это очень полезное изобретение в течение многих лет. Сам Отред говорил, что он «просто согнул и разогнул шкалу Гюнтера в кольцо», а также был убежден, что «истинное искусство математики не нуждается в инструментах». «, их использование считается допустимым только после изучения искусства. Однако его ученик настаивал на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский язык брошюру под названием «Круги пропорции и горизонтальный инструмент», в которой описывалась логарифмическая линейка.
Круговая логарифмическая линейка КЛ-1
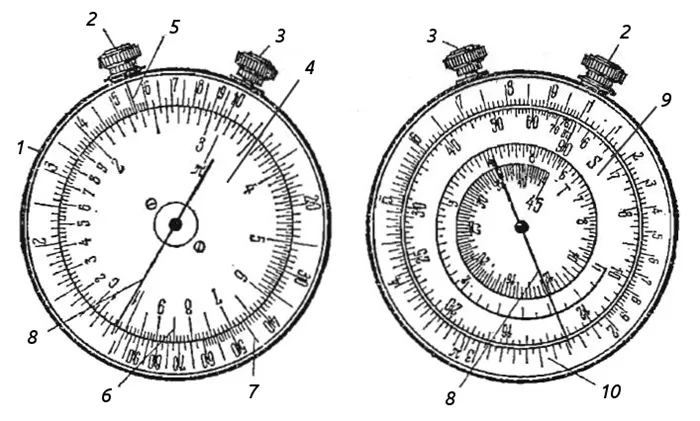
Линейка очень похожа на механический секундомер, за исключением того, что у нее нет механизма, а вместо ручек — поворотные головки, одна из которых вращает стрелки, а другая двигает циферблат.
В отличие от обычных логарифмических линеек, она не может считать логарифмы и кубы, точность на одну цифру меньше, и ее нельзя использовать как обычную линейку (и нельзя поцарапать спину), но она очень компактна, ее можно носить в кармане.

Быстрые вычисления
Прилагаемая инструкция (ниже) предлагает выполнять умножение и деление в три этапа: повернуть подвижную шкалу к указателю, повернуть стрелку на нужное значение и повернуть шкалу на другое значение. Однако гораздо интереснее использовать обе шкалы, подвижную и неподвижную на обратной стороне линейки, и выполнять вычисления в два движения. Можно вызвать весь диапазон значений сразу, просто повернув поворотную ручку, и сразу же считать значения.
Для этого поместите на неподвижную шкалу либо множитель (в случае умножения), либо делитель (в случае деления) и, повернув линейку, поместите второй множитель на стрелку или делитель на указатель и сразу же прочитайте результат, повернув подвижную шкалу. Поверните колесо дальше и сразу же считайте другие значения операции. Обычный калькулятор не может этого сделать.
Дюймы в сантиметры
Например, нам нужно перевести сантиметры в дюймы или наоборот. Для этого поверните головку с красной точкой на фиксирующей стрелке, чтобы установить значение 2,54. Затем посмотрим, сколько сантиметров на 24-дюймовом экране — повернем головку с черной точкой на подвижном циферблате и установим стрелку на 24, и прочитаем значение неподвижного указателя 61 см (2,54*24 = 60,96). Таким образом можно легко находить обратные величины, например, чтобы узнать, на сколько дюймов наш телевизор 81 см, мы ставим значение 81 на неподвижном указателе с черной точкой на шкале и читаем значение 32″ (81/2,54 = 31,8898) по стрелке.
Градусы Фарингейта в градусы Цельсия
Установите 1,8 на фиксированной шкале, вычтите 32 из Фаренгейта и установите полученное значение против фиксированного указателя, считайте Цельсий на указателе. Для обратного расчета установите значение в индексе и прибавьте 32 к значению в индексе.
20*1.8+32 = 36+32 = 68
(100-32)/1.8 = 68/1.8 = 37.8 (37.7778)
Мили в километры
Установите значение 1,6 на фиксированной шкале и поверните подвижную шкалу, чтобы получить мили в километрах или километры в милях.
Вычислите ускорение машины времени в фильме «Назад в будущее»: 88*1,6=141 км/ч (140,8).
Время и расстояние от скорости
Чтобы узнать, сколько времени потребуется, чтобы проехать 400 км со скоростью 60 км/ч, установите 6 на неподвижном циферблате на 6 и поверните подвижный циферблат на 4. Мы получим 6,66 часа (6 часов и 40 минут).
- Корпус.
- Головка с черной точкой.
- Головка с красной точкой.
- Подвижный циферблат.
- Неподвижный указатель.
- Основная шкала (счетная).
- Шкала квадратов числа.
- Стрелка.
- Неподвижный циферблат.
- Счетная шкала.
ПРЕДУПРЕЖДЕНИЕ Не допускается извлекать головки из корпуса.
Круглая логарифмическая линейка «КЛ-1» предназначена для выполнения наиболее часто используемых математических операций: Умножение, деление, комбинированные операции, приведение к квадратному корню, извлечение квадратного корня, определение тригонометрических функций синуса и тангенса и соответствующих обратных тригонометрических функций, вычисление площади круга.
Считывающее устройство состоит из корпуса с двумя головками, 2 циферблатов, один из которых вращается черной головкой, и 2 стрелок, вращаемых красной головкой. Напротив черной заводной головки над подвижным циферблатом находится неподвижная стрелка.
Подвижный циферблат имеет 2 шкалы: внутреннюю основную счетную шкалу и внешнюю цифровую квадратную шкалу.
На неподвижной шкале имеется 3 шкалы: внешняя шкала — измеряемые величины, аналогичная внутренней шкале на подвижной шкале, средняя шкала «S» — угловые величины для отсчета их половин и внутренняя шкала «T» — угловые величины для отсчета их касательных.
Математические операции с линейкой «CL-1» выполняются следующим образом:
I. Умножение
- Вращением головки с черной точкой повернуть подвижный циферблат до совмещения первого сомножителя по счетной шкале с указателем.
- Вращением головки с красной точкой совместить стрелку с отметкой «1».
- Вращением головки с черной точкой повернуть подвижный циферблат до совмещения второго сомножителя по счетной шкале со стрелкой.
- Против указателя по счетной шкале отсчитать искомое значение произведения.
II. Деление
- Вращением головки с черной точкой повернуть подвижный циферблат до совмещения делимого по счетной шкале с указателем.
- Вращением головки с красной точкой совместить стрелку с делителем по счетной шкале.
- Вращением головки с черной точкой повернуть подвижный циферблат до совмещения отметки «1» со стрелкой.
- Против указателя по счетной шкале отсчитать искомое значение частного.
III. Комбинированные действия
- Вращением головки с черной точкой повернуть подвижный циферблат до совмещения первого сомножителя по счетной шкале с указателем.
- Вращением головки с красной точкой совместить стрелку с делителем по счетной шкале.
- Вращением головки с черной точкой повернуть подвижный циферблат до совмещения второго сомножителя по счетной шкале со стрелкой.
- Против указателя по счетной шкале отсчитать окончательный результат.
IV. Возведение в квадрат
- Вращением головки с черной точкой повернуть подвижный циферблат до совмещения значения числа, возводимого в квадрат, по счетной шкале с указателем.
- Против того же указателя по шкале квадратов прочитать искомое значение квадрата этого числа.
V. Извлечение квадратного корня
- Вращением головки с черной точкой повернуть подвижный циферблат до совмещения значения подкоренного числа по шкале квадратов с указателем.
- Против того же указателя по внутренеей (счетной) шкале прочитать искомое значение квадратного корня.
Логарифмическая линейка состоит из двух основных частей:
Основание имеет форму обычной линейки, но в середине имеется прорезь, через которую скользит ползунок. Эти две части накладываются друг на друга в определенных точках для облегчения расчетов.
Линейка была изготовлена из прочной, устойчивой к истиранию древесины. Для этой цели часто использовалось грушевое дерево. Шкалы и деления были выбиты и залиты краской, чтобы надписи не исчезали с поверхности линейки. На линейке было маленькое окошко, сделанное из пластика или железа и стекла. Свобода движения была только в продольной оси.
Как работает логарифмическая линейка?
Линейка имеет в общей сложности 7 шкал. 4 из них отмечены на базе и 3 на курсоре. Вдоль боковых граней нанесена обычная сантиметровая разметка. Чтобы вы могли ориентироваться в весах, они обозначены стандартными символами:
- C, D – на нижней части движка, и под ним на основной части линейки – главные шкалы;
- K – кубическая шкала;
- A – квадратичная;
- B – аналогичная, вспомогательная;
- L – значения логарифмов;
- Sin – верхняя, значения синусов (косинусов может быть ниже);
- Tg – тангенсы.
Имена и номера могут незначительно отличаться. Подвижная часть может быть снята, а шкалы отмечены на обратной стороне.
Как считать логарифмической линейкой
Для правильного расчета числа, необходимые для подсчета, должны быть выровнены в окне, если оно есть, или на размеченной линии. Предположим, необходимо умножить число 180 на 0,4, тогда нужно действовать по алгоритму:
- на шкале D расположено 1,8;
- сдвинуть планки так, чтобы 1 на шкале C совпало с 1,8, вернее с десятичной ее частью – малый восьмой штрих после единицы;
- переместить металлический указатель с окошком так, чтобы его метка стояла на 4 по шкале C, тогда на шкале D, она будет указывать в районе 7,2;
- получается верное равенство: 180 * 0,4 = 72.
Логарифмическую линейку можно использовать для быстрого выполнения умножений и других математических операций. Кстати, учителя не запрещают использовать его на уроках. Хотя многие новые учителя не знают, что такое логарифмическая линейка.
Формулы для решения геометрических задач в правильном треугольнике.








